
L'unico vero videocorso in Italia per preparare il tuo esame di Matematica
DURATA:
13 ORE
ISCRITTI:
+50
VOTO:
5/5

A chi si rivolge "KEEP CALM AND LEARN MATH"
Il corso è stato creato dopo migliaia di ore di lezioni private
Pensi (erroneamente) di
non essere portato/a per la Matematica
Hai difficoltà con gli esercizi
Hai già provato a dare quest'esame, ma senza successo
Cerchi qua e là su internet, ma non trovi un programma strutturato e organizzato
"Keep Calma and Learn Math" è la soluzione per te
Cosa Otterrai con KEEP CALM AND LEARN MATH
Basta esercizi che non tornano, teoremi impossibili da capire, o appunti del compagno

Spiegazione step by step degli esercizi
Per poter passare Matematica devi saper fare gli esercizi, lo sappiamo.
Molti provano ad impararli a memoria, ed è qui che si fregano da soli.
Con "Keep Calm and Learn Math" vedrai il corretto svolgimento di ogni esercizio, step by step, in modo da capirli, e saper risolvere ogni esercizio che ti capiti davanti

Teoremi spiegati in maniera semplice
"E se all'esame mi dovesse chiedere la spiegazione di un teorema?"
Nessun problema, con "Keep Calm and Learn Math" avrai la spiegazione semplice dei teoremi più richiesti ad un esame di Matematica.
Sotto puoi vedere il programma
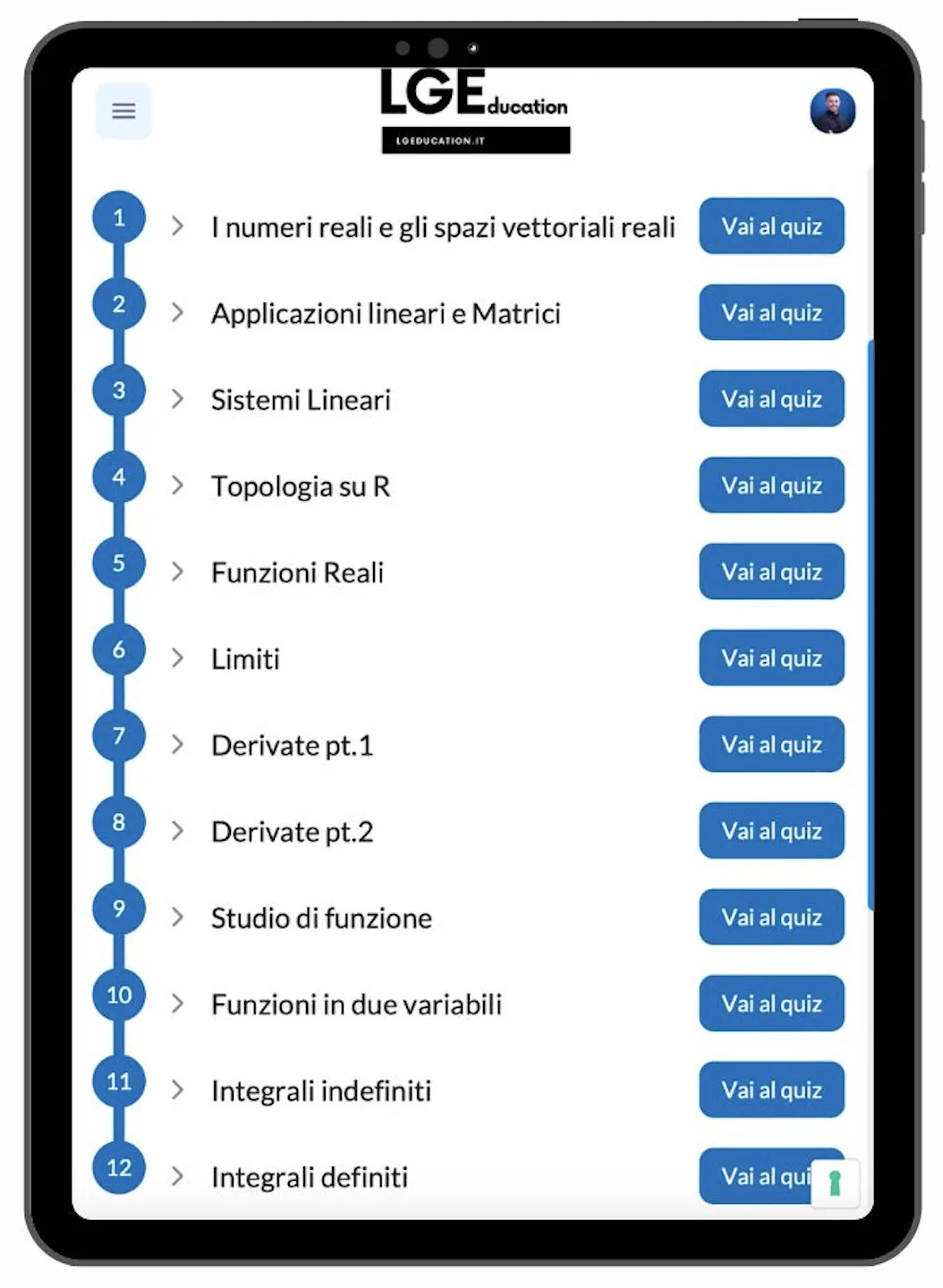
Programma strutturato
Molti cercano su internet, navigando qua e là ma senza avere un programma.
In "Keep Calm and Learn Math" troverai coerenza tra le definizioni e un programma già strutturato che devi solo studiare
Supera una volta per tutte Matematica con KEEP CALM AND LEARN MATH

Ecco il programma di KEEP CALM AND LEARN MATH
Tutto quello di cui hai bisogno, lo trovi qui.
I numeri reali e gli spazi vettoriali reali
Parte 1 - INTRODUZIONE: Introduzione sugli spazi vettoriali con definizione e prime proprietà
Parte 2 - RELAZIONE TRA VETTORI + ESERCIZIO: Combinazioni lineari, vettori linearmente dipendenti o indipendenti, prodotto scalare tra vettori, e molto altro…
Applicazioni lineari e Matrici
Parte 1 - INTRODUZIONE: Introduzione alle Matrici, alle Matrici particolari e alle loro applicazioni
Parte 2 - INVARIANTI CON ESERCIZI: Definizione e calcolo di determinante, rango e matrice inversa
Sistemi Lineari
Parte 1 - DEFINIZIONI E SISTEMI OMOGENEI: Cos'è un sistema lineare, terminologia, cos'è un sistema omogeneo, e perché è sempre possibile.
Parte 2 - SISTEMI NON OMOGENEI + ESERCIZIO: Teorema di Rouché-Capelli, metodi di risoluzione, e esercizio.
Topologia su R
Parte 1 - INTRODUZIONE: Concetti di distanza, intorno, intervallo, sup, max, inf, min, insiemi limitati.
Parte 2 - ALTRI ELEMENTI + ESERCIZIO: Insiemi aperti e chiusi, punti interni/esterni/isolati/di frontiera/di accumulazione
Funzioni Reali
Parte 1 - INTRODUZIONE: Definizioni riguardanti le funzioni in generale: dominio, insieme delle immagini, iniettività, suriettività etc..
Parte 2 - FUNZIONI ELEMENTARI E TRASFORMAZIONI: Definizione delle varie funzioni elementari e grafici deducibili da esse + esercizio calcolo del dominio
Parte 3 - MONOTONIA E CONCAVITA’: Definizione di monotonia e di concavità, massimo e minimo. Esercizio su massimo e minimo di una funzione
Limiti
Parte 1 - INTRODUZIONE: Come definire il limite di una funzione in un punto di accumulazione per il suo dominio
Parte 2 - TEOREMI: Come calcolare il limite di una funzione in un punto, con particolare attenzione alle forme indeterminate
Parte 3 - ESERCIZI: Vedremo vari esempi di calcolo di limite e di calcolo di asintoti di una funzione
Derivate pt.1
Parte 1 - INTRODUZIONE: Definizione di derivata come limite del rapporto incrementale, interpretazione grafica, operazioni fondamentali, ed esempi
Parte 2 - TEOREMI + ESERCIZIO: Derivata della composizione, della funzione inversa, Teoremi di Lagrange, Rolle, Cauchy e De L'Hopital.
Derivate pt.2
Parte 1 - FUNZIONI ELEMENTARI: Dopo aver rivelato le derivate delle principali funzioni elementari, studiamo i punti stazionari di una funzione, la monotonia e la convessità
Parte 2 - POLINOMI DI TAYLOR E MC LAURIN: Definiamo e calcoliamo i polinomi di Taylor e Mc Laurin, ne studiamo le proprietà e vediamo alcuni esempi
Studio di funzione
Parte 1 - INTRODUZIONE: Come determinare il dominio, il segno, le intersezioni con gli assi, i punti di discontinuità e gli asintoti di una funzione.
Parte 2 - STUDIO LOCALE E GRAFICO: Come determinare la monotonia, eventuali massimi e minimi, la convessità, eventuali punti di flesso, e il grafico qualitativo di una funzione
Parte 3 - ESERCIZIO: Svolgiamo assieme lo studio di una funzione
Funzioni in due variabili
Parte 1 - INTRODUZIONE: Come determinare analiticamente e graficamente il dominio di una funzione in due variabili. Come rappresentarne il grafico come superficie e mediante le curve di livello.
Parte 2 - OTTIMIZZAZIONE LIBERA: Come risolvere problemi di ottimizzazione libera
Parte 3 - OTTIMIZZAZIONE VINCOLATA: Come risolvere problemi di ottimizzazione vincolata
Integrali indefiniti
Parte 1 - LE PRIMITIVE: Definizione di una primitiva, integrale indefinito, caso delle funzioni elementari
Parte 2 - METODI DI INTEGRAZIONE: Integrazione per sostituzione, integrazione di funzioni razionali, integrazione per parti
Parte 3 - ESERCIZI: Calcolare integrali indefiniti con i metodi spiegati
Integrali definiti
Parte 1 - DEFINIZIONE E PROPRIETA’: Il problema del calcolo di aree; l'integrale definito come area; definizione formale, teorema del calcolo; proprietà
Parte 2 - TEOREMA DEL VALOR MEDIO: Enunciato, dimostrazione ed esempi di utilizzo del Teorema del Valor Medio Integrale

Riceverai un attestato alla fine del videocorso KEEP CALM AND LEARN MATH

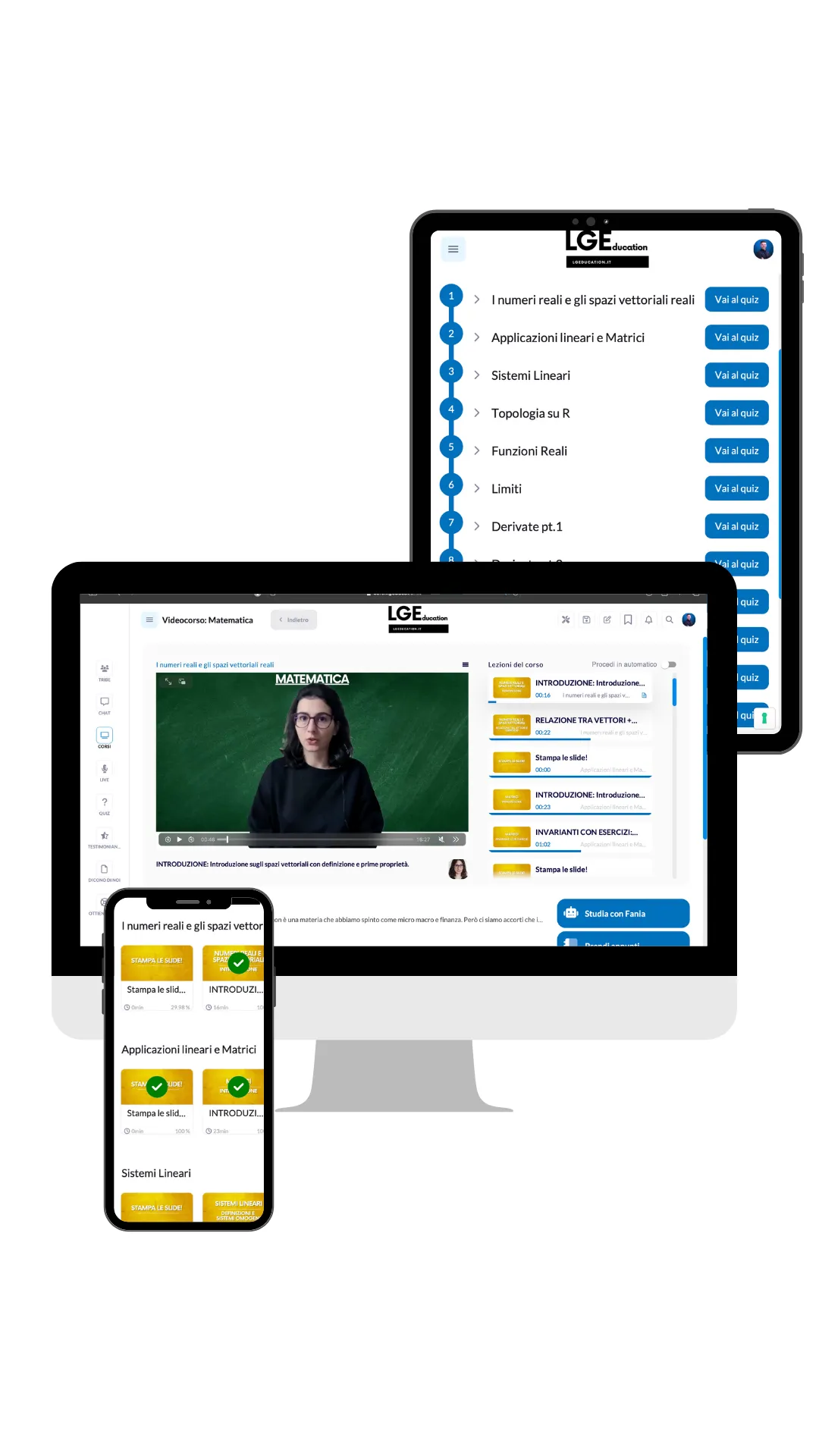
BONUS ESCLUSIVI
Tutti i nostri appunti/slide: tutto il materiale di supporto (slide e appunti) che utilizzo durante il videocorso, sarà a tua disposizione tra gli allegati!
Esercitazioni aggiuntive: se vuoi allenarti con un argomento in particolare, puoi farlo con esercizi aggiuntivi che ti faccio trovare direttamente negli allegati, per la maggior parte con le soluzioni!
Sezione dei quiz: avrai a disposizione 10 quiz a crocette per ogni capitolo!
Per due motivi: primo perchè ci siamo accorti che gli studenti che fanno il quiz dopo aver studiato, riescono a fissare molto di più i concetti; in più, se hai crocette o "vero o falso" all'esame, con la nostra sezione dei quiz puoi allenarti facendo esercizi con risposte chiuse!

DOCENTE
Ciao! Sono Nirvana Coppola, tutor di Matematica presso LGEducation da più di un anno.
Con un PhD in Matematica conseguito presso la University of Bristol e una laurea magistrale dall'Università di Pisa, ho dedicato gran parte della mia carriera accademica all'insegnamento e alla ricerca in prestigiose istituzioni europee.
Questo videocorso è nato dalla mia passione per la didattica e dal desiderio di aiutare il maggior numero possibile di studenti di economia a superare l'esame di matematica con successo.
Con me, durante il corso, porterò non solo una solida competenza accademica, ma anche una metodologia innovativa e pratica.
Credo fermamente che la matematica non debba essere un ostacolo, ma un trampolino di lancio per raggiungere i propri obiettivi accademici e professionali.
Unisciti a me in questo percorso di scoperta e apprendimento!
"Keep Calm and Learn Math" è più di un semplice corso: è il tuo compagno di studio ideale per affrontare con serenità e successo il tuo esame di matematica.
Cosa dicono di noi
Ecco l'esperienza solo di alcuni dei nostri studenti...
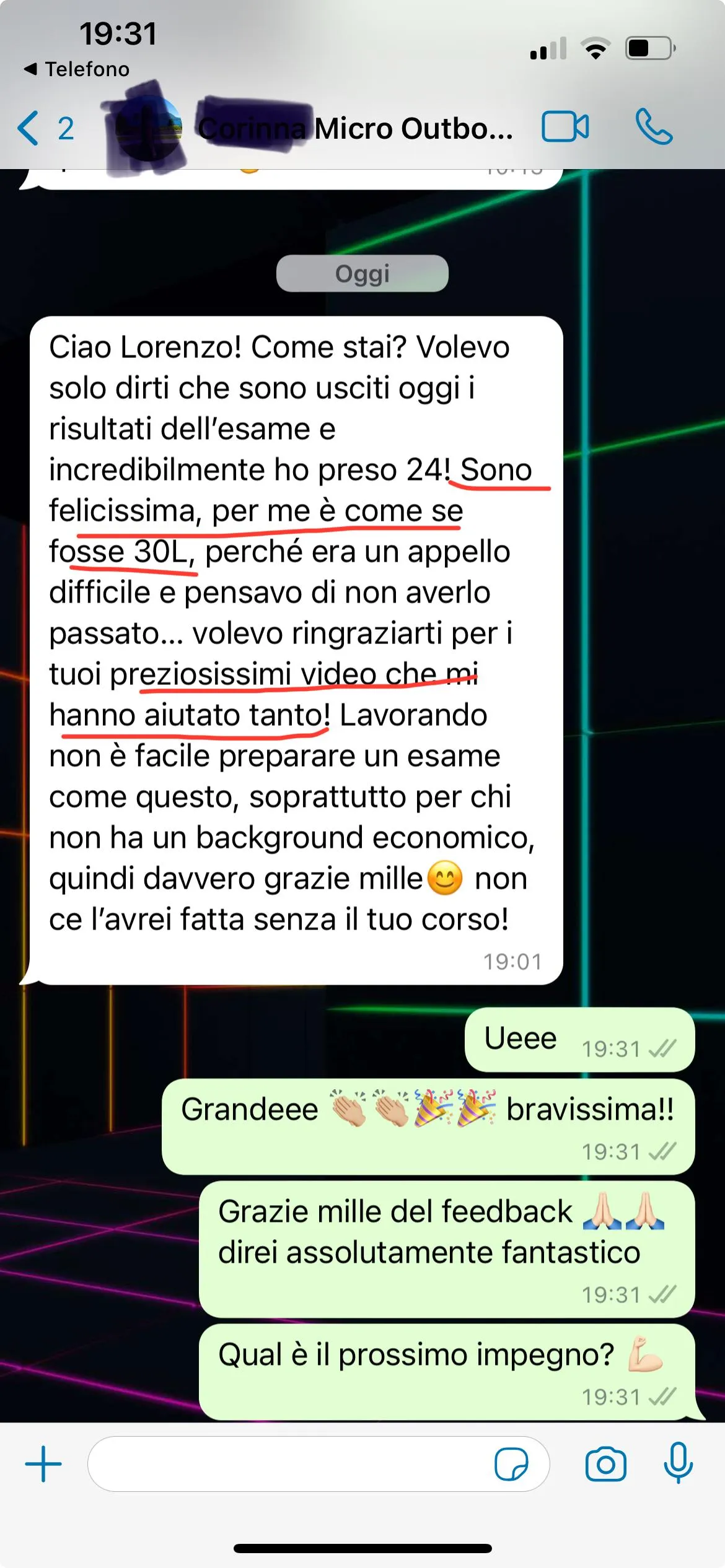
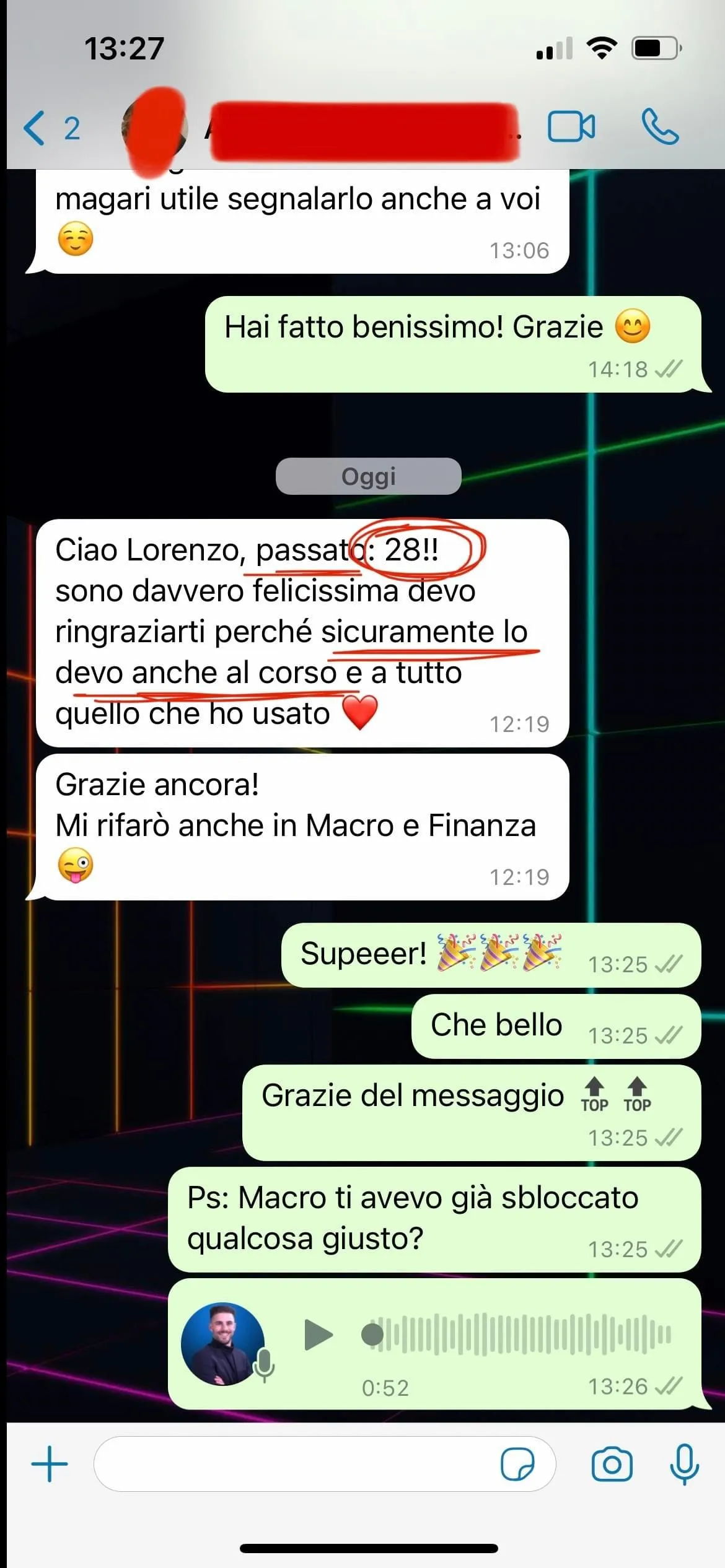

Adelaide - Economics and Management, Università Cattolica
Alessandro - Economia, Università di Pavia
Giorgio - Economia Aziendale, Università di Firenze
Valeria - Strategic Management, LUISS
Ege - Economics and Management, Università Cattolica
Thomas - Economia e Management, Università Bocconi
Alberto - Economia e Finanza internazionale, Bocconi
Edoardo - Economics and Management, Università Cattolica
Lorenzo - Scienze Politiche, Università di Milano
Lorella - Amministrazione Finanza e Controllo, Università Cattolica
Gianmaria - Economia e gestione aziendale, Università Cattolica
Chiara - Scienze Politiche, Università di Trieste
Chiara - Scienze Bancarie, Assicurative e Finanziarie, Università Cattolica
Ludovica - Scienza Internazionali, Università di Trieste
Tommaso - Economia Aziendale, Università Cattolica
Ascanio - Economics and Management, ESCP
Federica - Economia dell'impresa, Università di Bologna
Lorenzo - Economia e Management, Università Kore di Enna
Federica - Economics (Magistrale), Università Cattolica
Alessandro - Economia e Gestione Aziendale, Università Cattolica di Milano
Beatrice - Economics and Management, Università Cattolica di Milano
Davide - Economia e Gestione Aziendale, Università Cattolica di Milano
Alessandro - Business Economics, Università di Bologna
Cristina - Economia Aziendale, Università Federico II
Andrea - Economics and Management, Università Cattolica
Valeria - Economics and Management, Università Cattolica
Giulia - Economia e Management, Bocconi
Giacomo - Economia, Università Cattolica
Francesco - Economia dei mercati e degli Intermediari finanziari, Università Cattolica
Tommaso - Economics and Management, Università Cattolica
Anna - Economics and Management, Università Cattolica
Martina - Management dell'Informazione e della Comunicazione Aziendale, SAA di Torino
Matematica è nelle tue mani
Nessun costo nascosto - Accesso 24/7 - Pagamento in 3 rate con PayPal

FAQ
L'accesso è 24 ore su 24?
Certo! Una volta che hai le credenziali, potrai accedere quando vuoi.
Avrò l'accesso al videocorso per sempre o c'è una scadenza?
Nessuna scadenza!
Ma c'è veramente tutti gli argomenti di cui ho bisogno?
Abbiamo costruito questo prodotto dopo 3 anni di lezioni private, quindi abbiamo messo tutto quello che abbiamo fatto con gli studenti negli ultimi 3 anni (condensato). Posso dire che c'è veramente tutto quello che ti serve, però ovviamente, prima dell'acquisto fai un check con il programma del prof.
Ma il metodo utilizzato nei video del corso, è il solito metodo dei video Youtube?
Si! I video pubblicati su Youtube sono una piccolissima parte del videocorso, quindi il metodo che conosci da Youtube è il solito che trovi all'interno del videocorso
Ma se poi dopo il videocorso volessi fare delle lezioni private, posso aggiungerle?
Certo! Ti basterà contattarci a info@lgeducation.it o scriverci a +39 3716666435
Ma se avessi un problema, posso contattarvi?
Certo! Ti basterà contattarci a info@lgeducation.it o scriverci a +39 3716666435
Come funziona il metodo di pagamento?
Puoi pagare con carte o con PayPal
Come funziona il pagamento in tre rate?
Devi selezionare il pagamento con PayPal, e poi una volta fatto l'accesso all'app di PayPal prima dell'acquisto, se sei abilitato, ci sarà l'opzione "Paga in 3 rate"
Ma è veramente soddisfatto o rimborsato?
Certo! Se hai guardato tutti i video del videocorso Keep Calm and Learn Math, e non sei soddisfatto/a dei contenuti che hai trovato, puoi contattarci a info@lgeducation.it richiedendo il rimborso del corso. A quel punto sarai chiamato per capire cosa non ti ha soddisfatto, e capire come erogare il rimborso.